





 ransmission of signals without wire is done not by changing electric currents but by changing electromagnetic radiation. In magnetic resonance, radiation is not transmitted continuously but chopped into pulses. These pulses can be arranged in different pulse sequences.
ransmission of signals without wire is done not by changing electric currents but by changing electromagnetic radiation. In magnetic resonance, radiation is not transmitted continuously but chopped into pulses. These pulses can be arranged in different pulse sequences.
The form of the pulses is pivotal for its desired purpose. There are selective pulses which are used to create a single slice through an object to be examined, and non selective pulses which can excite the entire object; they are used in three-dimensional imaging.
Figure 01-08 shows a simple hard pulse which is of minor importance in magnetic resonance imaging. To improve the quality of pulses we have to shape them, i.e. vary their amplitude with time (Figures 01-08 and 01-09). Widely used pulse shapes include the Gaussian and the sinc pulses, the latter one giving a better slice profile.
The sinc pulse is defined as: sinc (x) = sin (x)/x
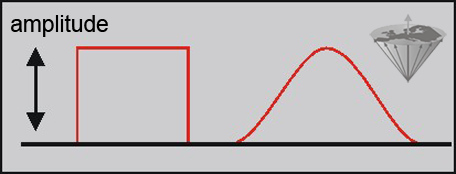
Figure 01-08:
Hard pulse (left) and shaped pulse (right).
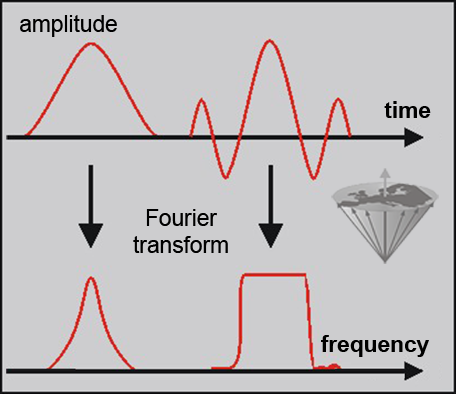
Figure 01-09:
Gaussian (left) and sinc pulses (right). Whereas the Fourier transform of the Gaussian pulse leads to a Gaussian shape, the Fourier transform of the sinc pulse comes close to a rectangular shape. This is more convenient in MR imaging because it allows a better definition of a slice through the human body.
Bandwidth is the range of frequencies included in the pulse. A certain bandwidth is needed for any signal. In general, bandwidth is directly proportional to the amount of data transmitted or received per unit time. In analog systems, bandwidth is defined in terms of the difference between the highest-frequency signal component and the lowest-frequency signal component.
A typical voice signal has a bandwidth of approximately three kilohertz (3 kHz); an analog television (TV) broadcast video signal has a bandwidth of six megahertz (6 MHz), some 2,000 times as wide as the voice signal.
Signals, for instance RF pulses, possess a certain waveform. Basically, they vary with time: they are a time function. However, it might be easier and better to work and analyze the properties of the pulse with respect to its frequency components.
This conversion can be achieved with a Fourier Transform (FT). The mathematics of the FT is complicated and intricate, but for our purposes it is only the results that count.
While the Fourier transform of a Gaussian pulse is also Gaussian, the FT of a sinc pulse approaches the ideal rectangular slice profile (Figure 01-09). However, even the sinc pulse is not the optimum pulse for a number of MR pulse sequences; thus, many alternatives have been developed.