mong all nuclei in the periodic table, ¹H, ¹³C, ¹⁹F, ²³Na, and ³¹P are among the most interesting for magnetic resonance imaging. All of these nuclei occur naturally in the body. The proton (¹H) is the most commonly used because the two major components of the human body are water and fat, both of which contain hydrogen. They all have magnetic properties which distinguish them from nonmagnetic isotopes.
Nuclei such as ¹²C and ¹⁶O which have even numbers of protons and neutrons do not produce magnetic resonance signals.
The hydrogen atom (¹H) consists of a single positively charged proton which spins around its axis. Spinning charged particles create an electromagnetic field, analogous to that from a bar magnet (Figure 02-02).
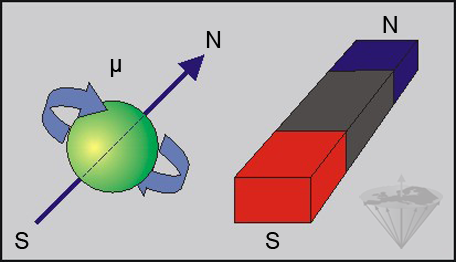
Figure 02-02:
A spinning charged particle possesses a characteristic magnetic moment μ and can be described as a magnetic dipole creating a magnetic field similar to a bar magnet (N = north, S = south).
When atomic nuclei with magnetic properties are placed in a magnetic field, they can absorb electromagnetic waves of characteristic frequencies. The exact frequency depends on the type of nucleus, the field strength, and the physical and chemical environment of the nucleus (Figure 02-03).
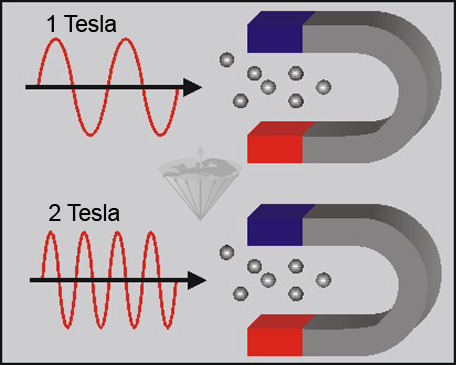
Figure 02-03:
The nuclei are able to absorb electromagnetic waves in both strong and weak magnetic fields. However, the absorption occurs at a field-strength-dependent frequency, which is higher in the strong magnetic field than in the weak magnetic field.
The absorption and re-emission of such radiowaves is the basic phenomenon utilized in MR imaging and MR spectroscopy. To understand the magnetic resonance phenomenon, two simple macroscopic parallels can be drawn:
First, let us consider a small magnetic needle placed in a magnetic field (Figure 02-04). If the needle is capable of rotating freely, it will orientate itself in the field in such a way that an equilibrium situation is attained. This equilibrium can be maintained indefinitely if no external forces influence the system.
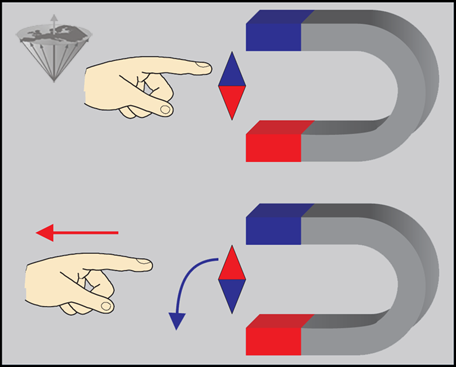
Figure 02-04:
The compass needle will seek the stable equilibrium state.
(Top) When it is turned around with a finger, energy is brought in and it will be in an unstable energy-rich position.
(Bottom) As soon as the finger is taken away, the needle will return to its stable state.
A second example illustrates the influence of the external strain on the frequency of the wave absorbed or re-emitted by the system. Imagine three identical guitar strings exposed to different tensions; the uppermost string of this instrument has no tension at all, the middle string weak tension, and the lowermost high tension. If we excite the strings, the resultant vibration is dependent on the tension of the strings (Figure 02-05).
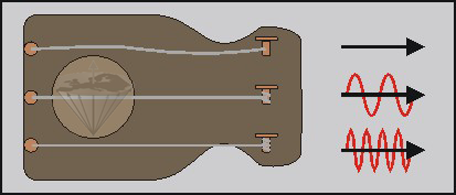
Figure 02-05:
A string (the nucleus) cannot vibrate without being exposed to tension (the external magnetic field). The higher the tension, the higher will be the frequency of the vibration.
In both examples, we have made comparisons between a macroscopic and the microscopic nuclear system. In the first example, we compared the nuclei with small magnet needles and in the second, with strings.
Such parallels provide a mental picture of the phenomenon, but have their shortcomings. One limitation of the models is that all physical phenomena on the molecular scale are quantified. For example, whereas an infinity of different orientations is possible for the magnetic needle, no smooth continuous transitions between the equilibrium state and the unstable, energy-rich state exist for the magnetic nucleus; instead, quantum mechanics predicts that only jumps between these two states are possible for nuclei with a spin of ½, such as protons (Figure 02-06) [spin of ½: ⇒ Holland 1993].
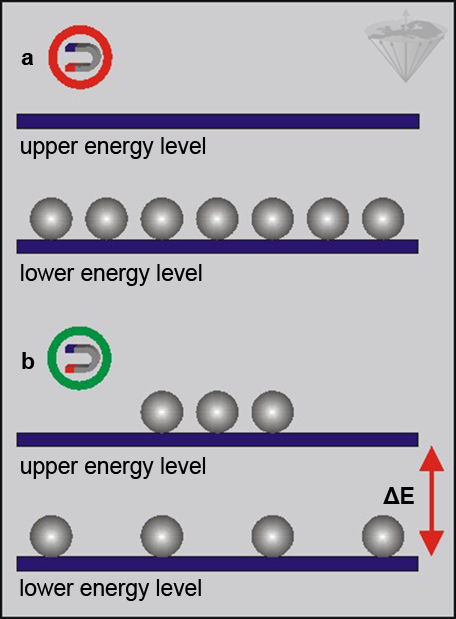
Figure 02-06:
(a) Protons outside a magnetic field, and
(b) protons in a magnetic field.
In the presence of a magnetic field, nuclei populate two distinct energy levels. The separation between these levels increases linearly with magnetic field strength, as does the population difference.
At equilibrium, we have a slightly larger population in the lower energy level, giving a net magnetization. To observe this population difference we have to provide an amount of energy equal to ΔE (the energy difference between the two levels).
|
Chapter 2 — Page 2 |
|
|---|