





 ntil now, only the microscopic behavior of the nuclei has been considered. However, any real sample contains a tremendous number of nuclei — a drop of water, for instance, contains about 10²¹ nuclei.
ntil now, only the microscopic behavior of the nuclei has been considered. However, any real sample contains a tremendous number of nuclei — a drop of water, for instance, contains about 10²¹ nuclei.
Macroscopically we observe the net effect of all microscopic events. In the presence of an external field, nuclei with magnetic properties similar to those of protons can occupy either the stable (and lower) energy state or be in the excited (upper) state, which has a slightly higher energy.
The energy difference between these two states is so small that the number of nuclei occupying each of the states is almost identical. Out of a million nuclei, there are only a few more low-energy nuclei than high-energy nuclei. Since the signal obtained in a magnetic resonance experiment depends on the difference in population between the two states, the resulting signal is very weak.
This is the reason why MR imaging has low sensitivity compared to, for instance, radioisotope studies. This handicap can be overcome by exploiting hyperpolarization. It allows an increase in signal enhancement by a factor of 100,000. However, these techniques are complex, require special equipment and are not available in clinical imaging.
Figure 02-09 shows that the sum of the nuclei precessing around the direction of the external field is equivalent to a single magnetic moment, called net magnetization. This represents the total magnetization of the population difference (those excess nuclei in the lower energy level at equilibrium). To detect this net magnetization, it is necessary to tip it away from the axis of the main field. This is achieved with an electromagnetic pulse at the resonance frequency.
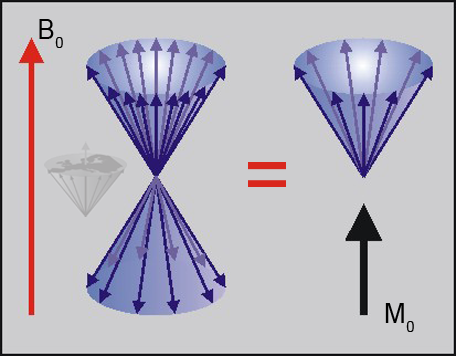
Figure 02-09:
Alignment of the individual magnetic moments with the external field. The population of the upper energy state is slightly higher. The sum of all individual components is the macroscopic magnetization or net magnetization M0.
According to the Boltzmann distribution, the number of spins in the upper energy level rises with increasing field strength.