• Chapter 2 • Contents
  The Basics Magnetic Properties of Nuclei The Boltzmann Distribution The Larmor Equation Resonance Magnetization The Rotating Coordinate System The Magnetic Resonance Signal Frequency Analysis: Fourier Transform

---

02-07 The Rotating Coordinate System

efore we try to explain the effect of a radiofrequency pulse on a spin sys­tem, we have to change our way of looking at this sys­tem. It is very dif­fi­cult to understand the movements within this system because the spin rotates around its own axis and precesses around the axis of the mag­ne­tic field B0 at the Lar­mor frequency.

The RF pulse adds another movement. To follow these movements requires a lot of ima­gi­na­tion (Figure 02-10).

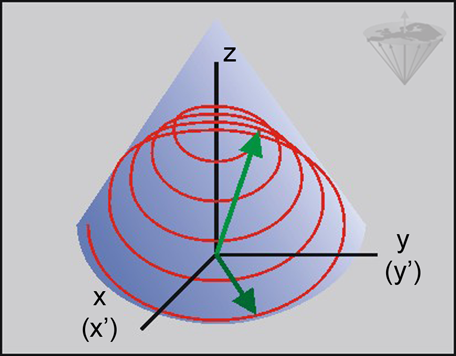
Figure 02-10:
The spiral motion of the tip of the mag­ne­ti­za­tion during RF excitation shown in a sta­ti­o­nary frame. The rotating frame depicts only the blue axes and the green arrows. To distinguish when we are using the ro­ta­ting frame of reference, we denote the x- and y-axes as x' and y'. The same pro­ce­dure can be used for z, but z and z' are iden­ti­cal.

However, if we try to look at the system from the perspective of a coordinate sys­tem ro­ta­ting at a frequency equal or close to the Larmor frequency, the si­tu­a­tion be­comes less complicated.

This may not seem obvious, but in fact we are doing this all the time. When a per­son walks by us, it is very easy for us to assess how much faster than us he is walk­ing. Yet, if we view the same action from outer space and have to take into account the rotation of the earth the problem would be much more com­pli­ca­ted.

We are, in fact, using a rotating frame of reference since we are rotating at the same rate. In NMR we can achieve this by using a frame of reference which is ro­tat­ing at the resonance (Larmor) frequency. On-resonance spins will be sta­ti­o­nary in this frame where­as off-resonance spins will rotate at a frequency which is the dif­fe­ren­ce between their frequency and the resonance frequency (Figure 02-11).

Figure 02-11:
Another example of a rotating (coordinate) system: Watching the horses on a merry-go-round from (a) far away and (b), after climbing aboard, from the merry-go-round itself. From outside, the horses look blurred and, if they are moving fast, it is not easy to distinguish them. If one’s point of reference is on the merry-go-round, it is much easier to distinguish the horses and their features.