o excite a spin system, one can expose the spins to a continuous electromagnetic wave of the right frequency. However, the method most commonly chosen for excitation of atomic nuclei in a magnetic field is to apply radiowaves of high intensity during a short period of time (pulsed magnetic resonance).
The frequency of these RF waves should be equal to, or close to, the Larmor frequency of the nuclei. Viewed from the rotating coordinate system (Figure 02-12 top), this results in a rotation of the magnetization away from the direction of the external field (Figure 02-12 center and bottom).
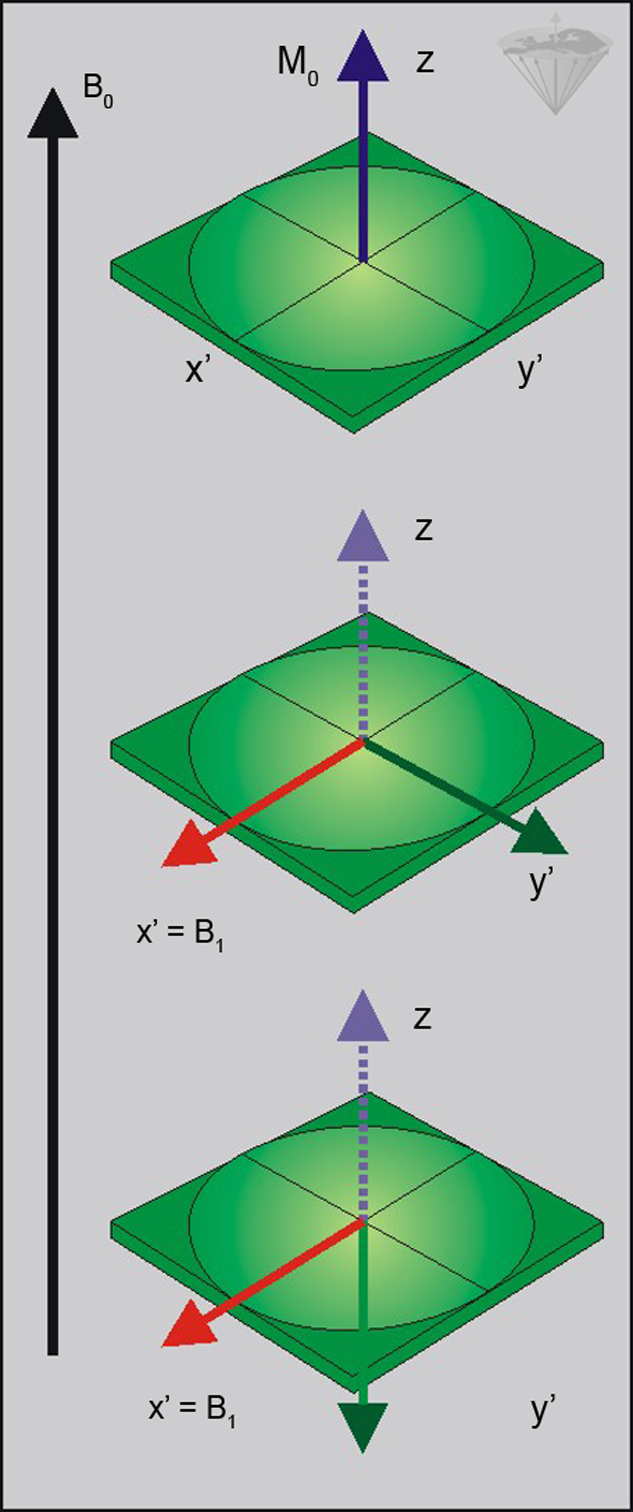
Figure 02-12:
Top: At equilibrium there is one stationary magnetic moment, M₀, directed along B₀.
Center: After being exposed to an RF pulse of an appropriate frequency, the magnetization (M₀) is tipped away from its equilibrium situation; in this case the pulse had tipped M₀ by 90° and is consequently called a 90° pulse.
Bottom: If a pulse lasting twice as long is applied a 180° pulse results, which inverts the magnetization.
To understand this, we have to remember that spins at the resonance frequency are stationary in the rotating frame, implying an effective magnetic field of zero. Therefore, the only field the spins experience is the B₁ field, which is the field created by the RF pulse. The spins rotate about B₁ in the same way as they rotate about B₀ in the stationary frame of reference.
In other words, prior to the RF pulse, the spins rotate about B₀ which is aligned along the z-axis (Figure 02-12 top). At this point, there is no net magnetization in any direction within the x'-y' plane. The RF pulse then tips the net magnetization away from the z-axis, towards the x'- and y'-axes of the rotating frame.
Following the pulse, the spins are still precessing about B₀, but their precession is no longer random; they precess in phase, and a net magnetization is produced in the x'-y' plane. This magnetization is aligned along the y'-axis following a 90° pulse along x'.
For a given RF intensity, the pulse angle is determined by the duration of the RF pulse. The duration of a 180° pulse is twice as long as that of a 90° pulse. Figure 02-12 (center) shows the situation for a 90° pulse, Figure 02-12 (bottom) for a 180° pulse that inverts the magnetization (green arrows).
In the standard stationary frame of reference, we now have a component of magnetization rotating at the Larmor frequency perpendicularly to B₀ (= longitudinal magnetization) in the x'-y' plane (= transverse magnetization). According to Faraday’s law of induction, this transverse magnetization can induce a voltage in the receiver coil surrounding our sample.
When the excitation pulse is switched off, the spins start returning to their equilibrium and emit a signal. The signal that is received from a homogeneous sample in a homogeneous magnetic field typically appears as shown in Figure 02-13a. It is called free induction decay, or FID, of the system. It looks like a damped oscillation.
If the magnetic field is not homogeneous, different parts of the sample experience different field strengths, and thus different parts of the sample will show different Larmor frequencies, leading to a more complicated FID (Figure 02-13b).
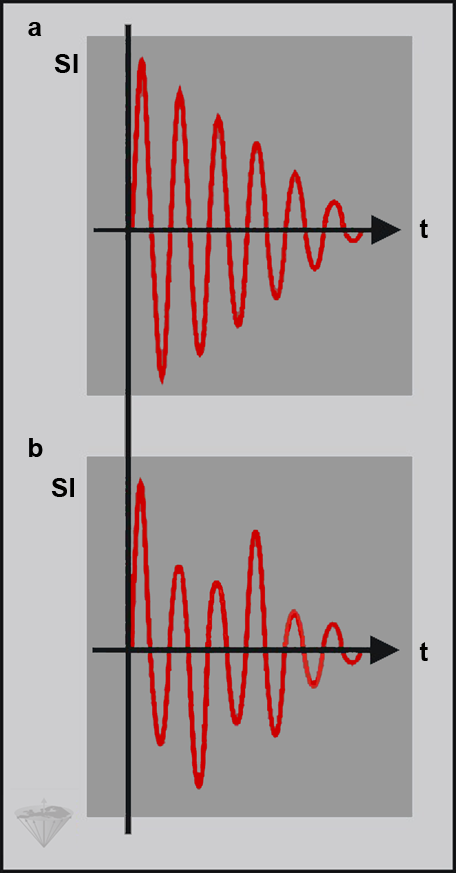
Figure 02-13:
The free induction decay (FID) (a) of a sample of pure water, (b) of a sample of water containing additional components. Usually, FIDs are far more complex than shown in these examples (SI = signal intensity; t = time).
|
Chapter 2 — Page 8 |
|
|---|