02-09 Frequency Analysis: Fourier Transform

The deconvolution of a FID is essential for the analysis of the information hidden in it. The idea of separating electromagnetic radiation into frequency com­po­nents is familiar to us through the use of a prism to split white light into its con­sti­tu­ent colors, each of which has a different frequency (Figure 02-14).

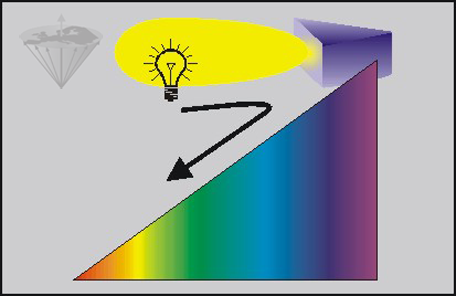
Figure 02-14: Frequency analysis: visible light is broken down into its components by a prism. The constituent colors are those of the rainbow. They have different frequencies.

The com­po­nents of a magnetic resonance signal can be analyzed by subjecting the signal to a Fourier transform. In this case, the prism is replaced by a computer.

It is more difficult to analyze the components of sound or, in our case, the mag­ne­tic resonance signal.

The physical phenomenon of a FID can be compared to the sound received from a bell. This sound is initialized by a short-lived impulse produced by the action of the clap­per. The resonating sound resulting from it is of high intensity at the beginning, but decays in intensity as a function of time.

The signals emanating from an inhomogeneous magnetic field can be com­pa­red to several bells tolling at the same time, creating a sound pattern which does not easily allow the differentiation of a single bell. Before it is possible to se­pa­ra­te the received oscillating signal into its components, it must be digitized, con­ver­ted into a binary se­quen­ce, and stored in a computer.

Applying a Fourier Trans­form (FT), one then can analyze the signal for its fre­quen­cy components and determine the intensity of each frequency. With a Fast Fourier Trans­form (FFT) algorithm, this may take only a few milliseconds. It is possible to analyze the frequencies of a number of bells tolling at the same time by measuring their com­bin­ed response at a particular frequency and then pro­cee­ding to the next frequency un­til the whole frequency range has been covered. This is analogous to the original mag­ne­tic resonance experiment.

However, if we excite and then measure all frequencies at the same time in the same experiment, we obviously greatly increase the efficiency of the ex­pe­ri­ment. In pulsed magnetic resonance, all frequencies of interest are excited by the pulse, and we rely on the Fourier transformation to sort out the intensity of response at each frequency (Fi­gu­re 02-15).

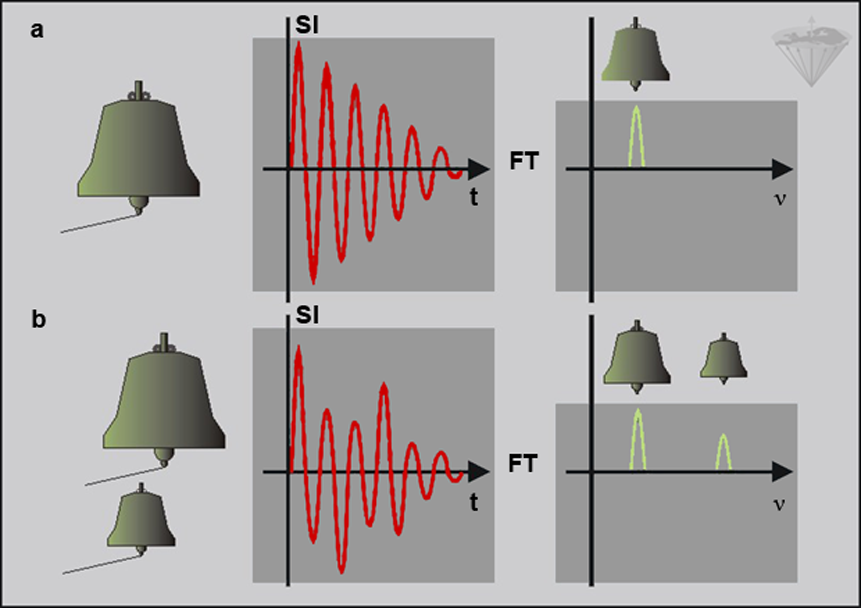
Figure 02-15:
The equivalent example: the sound wave originated by a single bell and by two bells of dif­fe­rent sizes. Tolling a single bell once gives a clean sound (not in reality, but for the sake of our ex­amp­le), while tolling several bells at the same time gives a mixed sound.

The Fourier transform (FT) of the signal emitted by a single bell (or a pure water sample in NMR) and two different bells (water containing different components in NMR) provide us with spectra showing the frequency content of the sound. The same mathematical analysis can be used for the FID.

(SI = signal intensity; t = time; ν = frequency).