06-08 Partial Fourier Imaging

To reduce the scan time, it is possible to omit some of the phase-encoding steps and use the acquired data to estimate the missing data, given that the data set has conjugate symmetry [⇒ MacFall]. The image can then be reconstructed in the normal manner. Ideally, it would only be necessary to acquire half the data set, but imperfections in the magnetic field and effects such as flow lead to phase errors. To compensate for these phase errors, it is necessary to collect slightly more than half the data set and then calculate a phase correction. If 70% or more of the raw data is acquired, it is not necessary to calculate a phase correction.

If used together with a spin-echo sequence, only 55% of the phase-encoding steps have to be acquired before we can accurately reconstruct the image. With gradient-echo techniques, a rather larger fraction of the data set is required for accurate reconstruction due to the larger phase errors arising from the field in­ho­mo­ge­neity errors in the gradient-echo signal. In both cases, the final images will have a reduced signal-to-noise ratio compared with images acquired using all the phase-encoding steps since the noise in the two halves of the partial Fou­rier image will be correlated.

06-09 Three-Dimensional Fourier Imaging

In the late 1970s and early 1980s, all original images acquired at Paul C. Lau­ter­bur’s laboratory were three dimensional (3D). Other research groups and ma­nu­fac­tu­rers introduced two-dimensional (2D) imaging because such images could be acquired faster and easier.

The 3D imaging methods available today are all based on 3D-Fourier re­con­struc­tion. The 2D spin-warp sequence can be extended to a 3D sequence by applying the RF pulse without a slice gradient, causing the whole sample to be excited. Three-dimensional imaging usually does not use spin-echo sequences because of the long scan time, but rather gradient-echo (GRE) or rapid spin- echo (RSE/FSE/TSE) sequences.

To obtain spatial information in what was previously the slice direction, we have to apply a second phase-encoding gradient. To obtain full spatial encoding of the volume, it is necessary to step the second phase-encoding gradient through its full range of values for each step of the first phase-encoding gradient.

The disadvantage of 3DFT imaging is that unless the repetition time is very short, the scan time will be excessively long. The main advantage of the 3D technique is that it has a signal-to-noise advantage over 2D techniques (if the voxel size is kept constant, the signal-to-noise ratio improves by the square root of the number of slices). Other advantages are that the slices are contiguous (which is not the case with multiple-slice techniques), that any desired slice orientation can be reconstructed from the data set, that very thin slices can be obtained, and that the slice profile of the 3D set is rectangular.

Among the additional problems with 3D imaging are that data processing requirements are greatly increased, that viewing 3D data sets with typically 64-128 images created during one data acquisition generally requires a separate workstation, and that for each 3D image set we have only one type of contrast.

A compromise between full 3D and 2D imaging is to excite a thick slice (slab), which is then sub-encoded into slices using a 3D sequence (Figure 06-22). This allows the 3D region to be accurately defined, but if used with only a small number of phase encodings in the third dimensions, significant ringing artifacts can occur. The slabs must have a good slice profile; otherwise some of the slices must be used to encode the edges of the slabs to avoid ringing artifacts [⇒ Johnson].

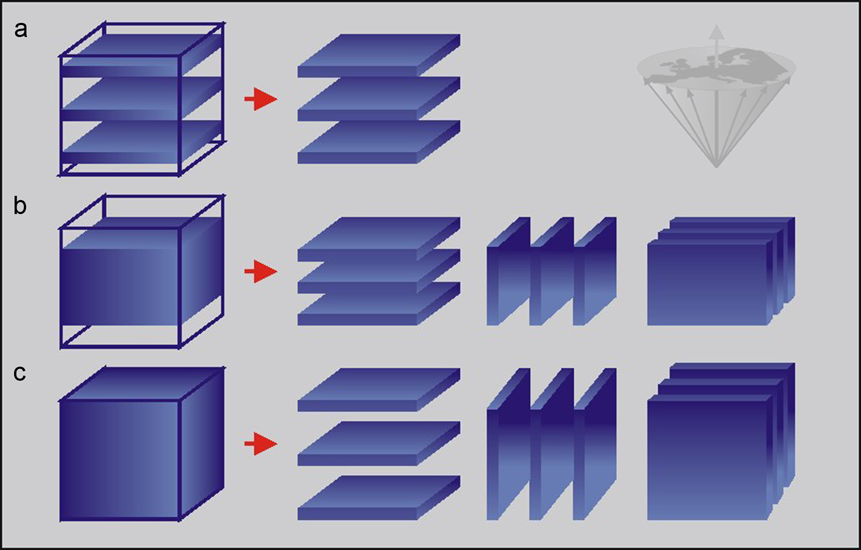
Figure 06-22:
(a) 2D multiple slices; (b) 3D slab, which can be used to create 2D slices; (c) 3D volume, which can be used to calculate slices in any direction of the entire volume.