n advanced approach for image acquisition uses multiple RF receiver coils with independent RF pathways, known as phased array or synergy surface coil arrays (see Chapter 3).
In these arrays, each individual coil produces a signal of its own. Several independent image data sets can be acquired at a time and, after postprocessing, synthetized into a single image.
Commonly, a combination of such overlapping multiple receiver coil elements is utilized to improve the signal-to-noise ratio (Figure 06-23).
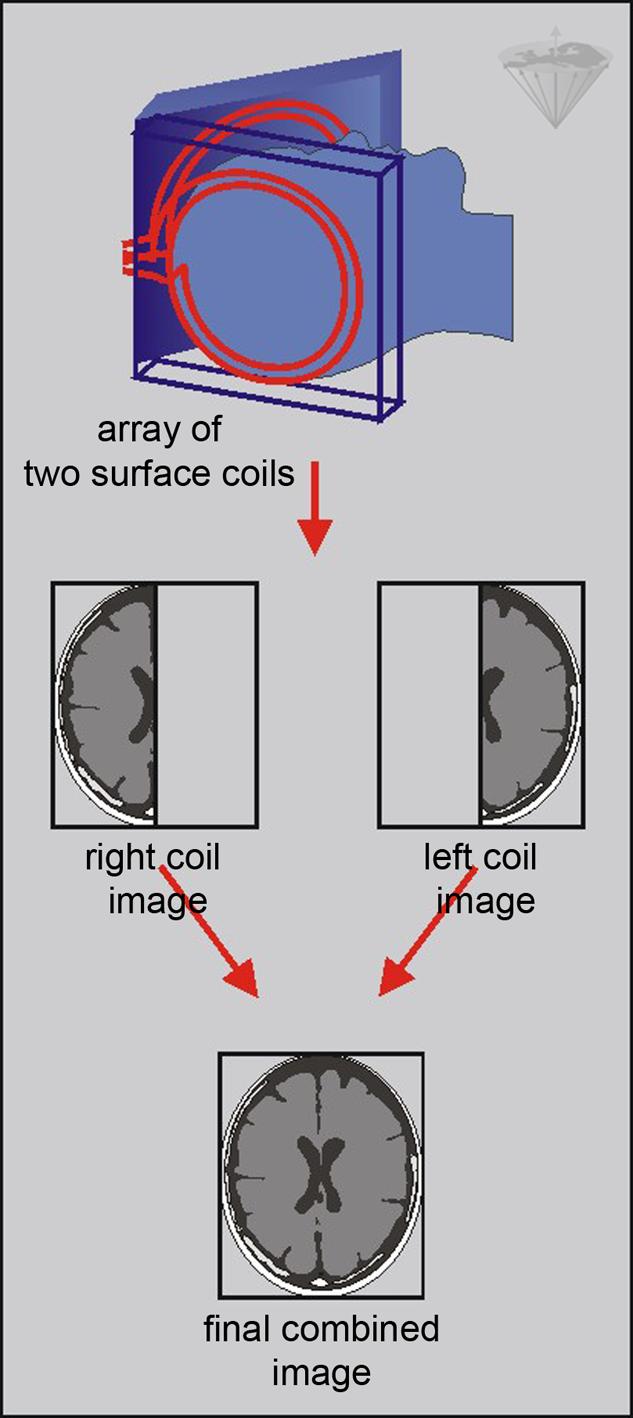
Figure 06-23:
Parallel imaging with an array of two coils: each coil provides half of the field-of-view of the final image; thus, only half of the phase-encoding steps have to be acquired.
In the sensitivity profiles of the individual receiver coil elements there is spatial information contained, and multiple phase-encoded data can be derived at the same time. Thus, the number of gradient-based spatial encoding steps can be decreased and conventional Fourier encoding reduced.
This procedure is based upon dedicated adjuvant reconstruction algorithms, among them SENSE (Table 06-01) [⇒ Pruessmann 1999], and SMASH. These algorithms must not be confused with pulse sequences although their acronyms sound similar. In principle, they can be applied to any imaging sequence; contrast behavior does not change.
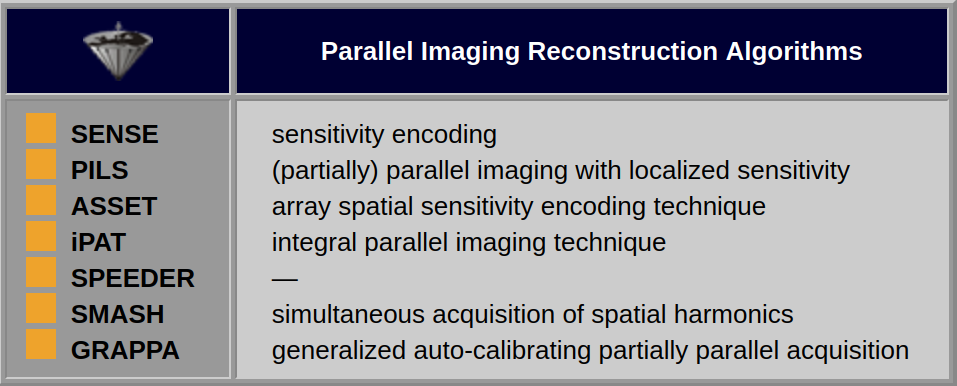
Table 06-01:
Adjuvant parallel imaging reconstruction algorithms.
The names are different, but the approach is the same.
Both SMASH and SENSE algorithms reconstruct missing data to obtain an image without backfolding artifacts. The way that this is actually done represents the main difference between the two techniques. SMASH will perform this calculation on the raw data, before the Fourier transform, while SENSE will work with the images obtained from the respective coils. SENSE and SMASH are based on knowledge of the sensitivity profiles of the individual coil elements.
This knowledge is acquired either through a very low resolution 3D volume scan (64×64×64 matrix) which then can be used for all consequent scans independent of orientation, or through adding some additional phase encoding steps to each reduced acquisition. Therefore, from a practical point of view, the first solution will be time effective if more scans are performed, the latter is to be preferred if only one scan is wanted.
SENSE, PILS, and ASSET reconstruct the final image from the sub-images produced by each coil after the Fourier transformation in the image domain, whereas GRAPPA reconstructs the Fourier plane of the image from the frequency signals of each coil before the Fourier transformation.
SENSE and its relatives work with most pulse sequences and clinical applications. Moreover, they also allow the user to choose between either increased spatial or temporal resolution [⇒ Blaimer 2004, ⇒ Larman 2007].
The downside of parallel imaging is that the signal-to-noise ratio is reduced compared to phased-array imaging. The reduction in signal-to-noise does no longer follow the common square-root dependence because of the non-Cartesian sampling and the noise correlation between pixels.
Critical Remarks. Since one can acquire an image with a full matrix in 2-3 minutes using GRE and TSE sequences, there is often no real need for parallel imaging and therefore a loss of signal-to-noise.
It is often used in dynamic imaging and 3D/4D imaging where saving time is important and one can afford to trade off some signal.
Compressed Sensing. To accelerate imaging beyond the gain achieved in parallel imaging, additional processing of image data by Compressed Sensing was introduced as a concept already used in a number of non-medical applications. It produces an image based on as few variables as possible: sparse data [⇒ Donoho 2006, ⇒ Lustig 2007, ⇒ Mairal 2012. An image is considered as 'sparse' when its informational content is represented by only a few pixels, while the contribution of the remaining majority of pixels is close to zero; the image is reconstructed from undersampled measurements to a "nearly perfect state" [⇒ Geethanath 2013].
There are no studies yet whether relevant diagnostic data are lost by such procedures.
|
|
|---|