ts flexibility distinguishes MR imaging from all other medical imaging modalities. The ultimate reason for this is the unique handling of MR raw data in an abstract data collection matrix called k-space, where the data stay to be deciphered. This space consists of the raw data that have been collected during image acquisition but have not yet been converted into the final anatomical image.
The motto in the foreword to this book fits very nicely with this chapter:
"Why, sometimes I’ve believed as many as six impossible things before breakfast."
The easiest way to deal with k-space is seeing and believing; this, however, is not very helpful when one wants to understand how some imaging techniques function and what their pitfalls are (Figure 07-01).
Of course, k-space behaves differently from cat eyes, but there are some similarities as will be explained in the text.
Figure 07-01:
There is something wrong here: we do not talk about CAT-scans in CAT-space — or do we?
The picture on the left was taken during daytime, the picture on the right at night. Look at the cat’s eyes: the pupils are small when there is a lot of light, but then they are wide with little light.
The central part of the retina displays extraordinary visual discrimination, thanks to the tiny size of the closely packed, light sensitive cones located there.
This area with maximum resolution covers only 1° of the eye’s field-of-view. At night, the periphery of the retina is used; it has an incredible sensitivity to light but a very poor ability to distinguish details.
First and foremost, a k-space is a mental concept. There is no hardware in an MR machine corresponding to it. It is a platform to collect, store, and process complex data. These data represent thousands of sine and cosine waves which build the MR image.
The term k-space is mathematical. The letter ‘k’ is used by mathematicians and physicists to describe spatial frequency, for instance, in the propagation of sound, light, or, in general, electromagnetic waves.
One way of understanding the concepts and mechanisms of k-space is looking at a different physical property which, perhaps, is simpler to imagine: the collection and processing of light by a lens, as Mezrich explains in his introduction to k-space [⇒ Mezrich 1995].
The processing of the incoming light to an image by the lens determines to a great extent its resolution, size, and contrast. The light passing through the lens is bent slightly in the center, increasingly towards the edges. In a perfect lens, the light will meet in one point, the focus, and then create an inverted image (Figure 07-02).
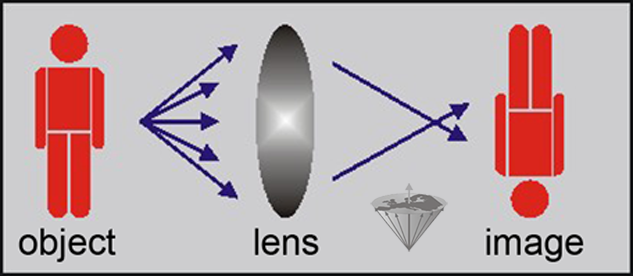
Figure 07-02:
Image processing by a lens.
The processing of the light data by a lens is more complicated than generally thought: there is no point-to-point correspondence between points within the lens — or within a center plane in the middle of the lens — and the final image created by the lens. All points within the lens process data from all points of the original object. However, for our purposes we could imagine such a center plane as the location where processing takes place (Figure 07-03).
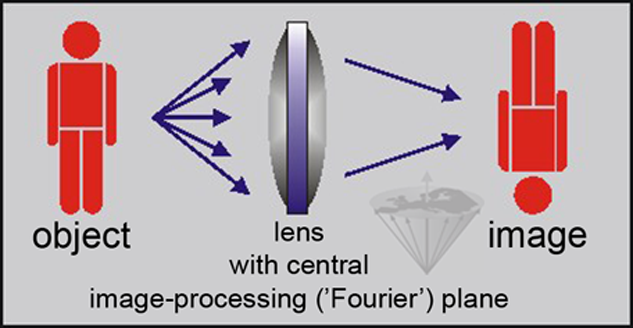
Figure 07-03:
Image processing by a lens with a fictitious image-processing plane.
Visible light actually consists of different frequencies. As we have already seen in Chapter 2, a prism can make a frequency analysis. A lens is more sophisticated. We can consider it as a special filter which, depending on its characteristics, lets some or all of these frequencies pass. It accepts signals, analyses them, processes them, and creates an image; basically, it performs a Fourier transform. We have assumed that the Fourier transform is accomplished in a fictitious central plane of the lens. In front of the lens, we can set instruments performing optical functions, for instance an iris, or we can change the size of a lens (Figure 07-04).
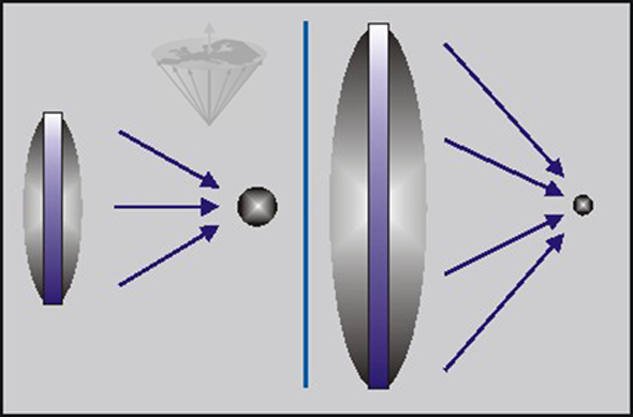
Figure 07-04:
Increasing the size of a lens with the same focus improves image resolution because the individual image points are smaller — the same holds for k-space: larger k-space with the same field-of-view means better spatial resolution of the image.
Changing the size of the lens or an iris influences the size of our processing plane. The steeper the angle the light makes within the lens, the sharper the focus will be; the larger the lens, the better image resolution will be. The sharpness of the final image is determined by the outer parts of our 'Fourier' plane. Points in the outer regions of the plane contribute more to image resolution than points close to the center because they allow higher spatial frequencies to pass through.
Lower spatial frequencies are closer to the center. Their main responsibility is the distribution of brightness and darkness. This means that they are responsible for image contrast.
|
|
|---|