• Chapter 7 • Contents
  Introduction The Optical Equivalent MR Imaging and k-Space Filling k-Space and Image Reconstruction 

---

07-04 Filling k-Space with Data and Image Reconstruction

n most MR imaging sequences applied in clinical routine today, raw data are placed in a rectangular k-space grid [⇒ Edelstein 1980].

For example: In a standard spin-echo sequence, each 90° pulse creates a new line (Figure 07-08). The length of the line is determined by the strength of the fre­quen­cy-en­cod­ing gradient and the sampling time, its position by the strength of the phase-encoding gradient.

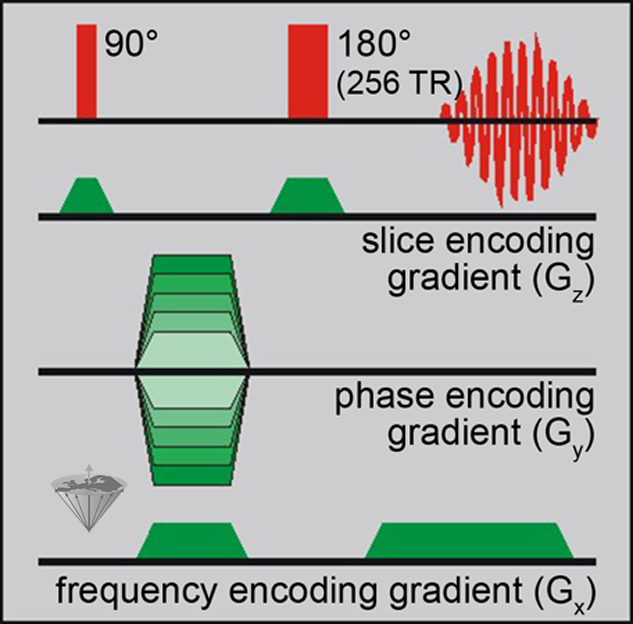
Figure 07-08:
Graphic depiction of a spin-echo pulse sequence.

The position of the line is determined as follows: After the initial 90° ex­ci­ta­tion pulse, the spins evolve in the direction given by the phase-encoding gradient Gy and the frequency-encoding gradient Gx (yellow arrow in Figure 07-09a). They are then turned around by the 180° pulse (red/magenta arrow). Then the fre­­quen­cy en­cod­ing gra­dient is switched on again and sampling starts. This is repeated for dif­fe­rent amp­li­tu­des of the phase-encod­ing gradient until k-space is filled (Figure 07-09b).

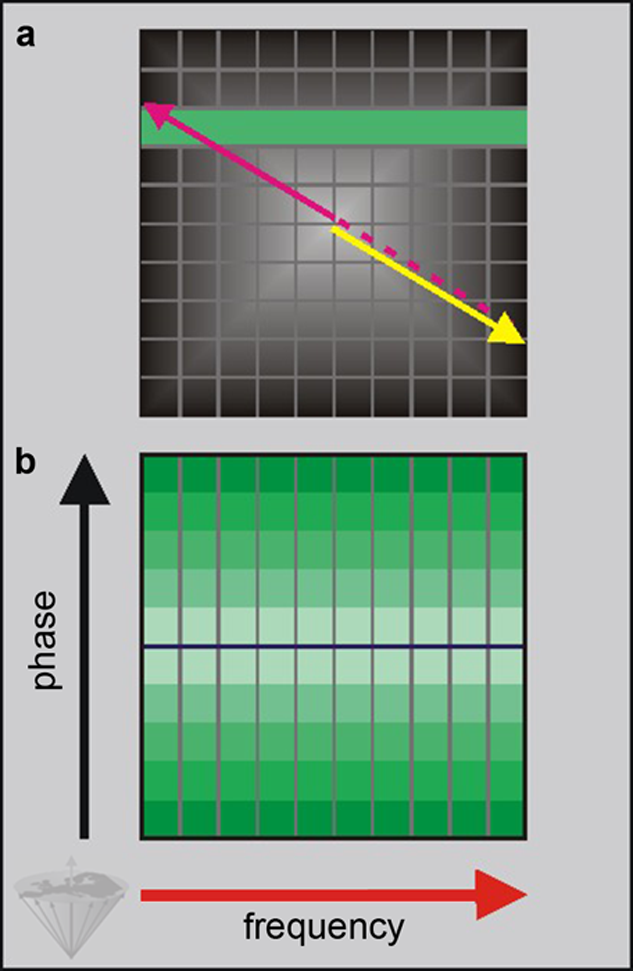
Figure 07-09:
Mapping of k-space in a spin-echo pulse sequence.
(a) Positioning of a single line.
(b) Filling of the entire k-space. Phase di­rec­tion: blue arrow, frequency direction: red arrow.
In conventional pulse sequences, such as the spin-echo sequence, one line of k- space is filled per re­pe­ti­tion time (TR) cycle (commonly there are 256 cycles per ima­ging experiment, not only ten as in this fi­gure).

The time needed for such an imaging experiment is the number of phase-encoding steps (NGy) multiplied by the repetition time (TR) and the number of excitations (NEX):

t = NGy × TR × NEX

Now we have filled the data matrix with each row containing information from one echo. Each data point is then Fourier-trans­formed in the x-direction, which leads to a new data matrix where every point in each column contains in­for­ma­tion stemming from a certain frequency; the phase infor­mation differs point-by-point per row.

The second Fourier transform is performed in the y-direction to extract phase in­for­ma­tion.

This again leads to a new data matrix con­taining combined phase and fre­quen­cy in­­for­ma­tion. The output is a matrix showing a modulus or magnitude image which cor­re­s­ponds to the bulk of MR signals from each point. Phase correction might be ne­ces­sa­ry to correct for phase jumps bet­ween 0° and 360°.

Among the main parameters influenced by k-space are the speed of ac­qui­si­tion, spa­tial resolution, field-of-view, contrast, and artifacts. Details can be found in some dedicated papers [⇒ Hennig 1999, ⇒ Mezrich 1995, ⇒ Pelc 1993, ⇒ Peters 1993].