





 ntil now we have focused entirely upon the methods with which we can excite the region of interest. In order to obtain an image of this region defining spatial distribution and other characteristics, we need to discuss the different methods for spatial encoding.
ntil now we have focused entirely upon the methods with which we can excite the region of interest. In order to obtain an image of this region defining spatial distribution and other characteristics, we need to discuss the different methods for spatial encoding.
These methods can be divided into two groups: frequency encoding and phase encoding.
Frequency encoding is conceptually the simplest of the two encoding methods: If a sample is placed in a homogeneous field, no information concerning the spatial location is present in the magnetic resonance signal, since all regions of the sample have the same Larmor frequency.
However, when a gradient is imposed on the sample, the magnetic resonance signal contains information about the spatial location of the resonating spins. If we rotate the gradient in all three dimensions, we can both distinguish different samples or different tissue contents in the body, as well as locate them in all three spatial dimensions.
Let us consider two water samples. They are displaced in both the x- and y-directions. When we apply only a gradient in the x-direction, we do not gain enough information to deduce their position in space.
However, if we perform the experiment three times with gradients applied in the x- y-directions respectively, then we have enough information to be able to estimate their positions (Figure 06-12).
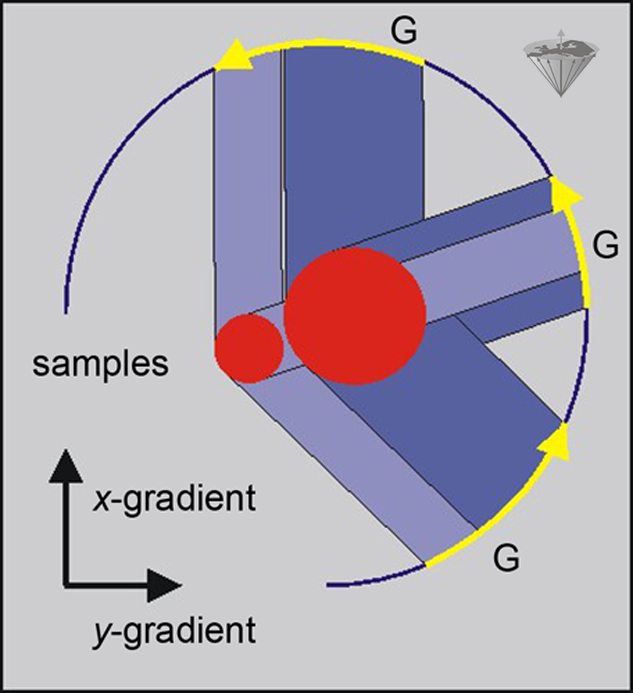
Figure 06-12:
By using field gradients along the x- and y-axes in three different experiments, the positions of two samples of water with displacement in both the x- and y-directions can be estimated.
The projection obtained through the use of a gradient can be thought of as being a shadowgram resulting from a light beam applied perpendicular to the gradient. Each projection thus shows the position of the object along a particular axis. In order to be able to calculate both the form and the position of one or more objects, it is necessary to measure a set of projections for angles between 0° and 180° with steps of 1° or 2° between projections. It is not necessary to cover the full 360° since this would simply duplicate the projections obtained over 180°.
The projections obtained in this way can then be mathematically processed to produce an image of the object. This approach is conceptually similar to that used in x-ray CT and was the method used for the very first demonstration of MR imaging [⇒ Lauterbur 1973]. The method is generally referred to as projection reconstruction or backprojection (Figure 06-13).
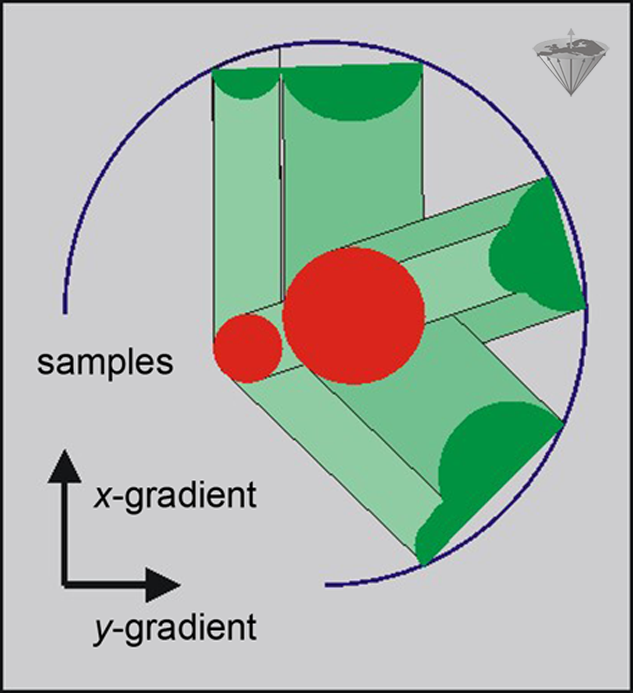
Figure 06-13:
Backprojection method: three projections of a sample allow the location of the objects and creation of a crude image. Additional projections will lead to a more exact definition of the shape of the objects.
Projection reconstruction was little used in clinical MRI, mainly because it is very sensitive to the effects of inhomogeneities in the main magnetic field. However, recent improvements in magnet technology have reduced the level of these imperfections, which has led to renewed interest it. One of the main potential applications for such techniques is in diffusion imaging, where the errors produced by motion seriously degrade the images acquired using other reconstruction schemes [⇒ Jung 1991].
In frequency encoding, the system is excited while no gradient is present; then the signal is recorded in the presence of a gradient. The phase encoding takes place before the signal is recorded, but again in the presence of a gradient.
Immediately after the excitation, the spins are coherent, no difference in phase has yet developed, and if we wait, natural T2 processes (and field inhomogeneities) will start acting on our sample, and some dephasing will start.
However, if we suddenly switch on a gradient, then the spins will start dephasing. The rate of dephasing will depend on the location of the individual spin and the strength of the gradient. The phase of the spins contains spatial information. Phase encoding compares the phase with an MR signal of the same frequency. The information can be recovered by a suitable application of the Fourier transformation.
To obtain a resolution of n pixels in the y-direction, we have to repeat the experiment n times. The phase gradient is changed (stepped) at each repetition with a certain increment. The changes in the phase gradient can be obtained by changing either the duration or the amplitude of the phase gradient.
The former method was the first to be suggested,1 but has the disadvantage of giving a different T2- (or T2*-) weighting to the different phase steps. Thus, the method of varying the amplitude of the phase gradient is preferable [⇒ Kumar 1975].
The effect of applying different gradients to samples at different positions is shown in Figure 06-14.
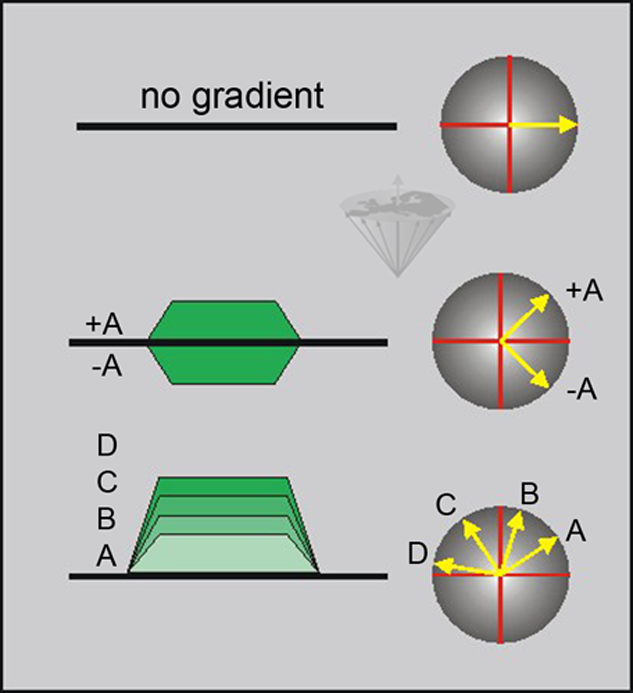
Figure 06-14:
The phase angle induced by a gradient depends on both the amplitude and the duration of the gradient. When using a constant duration for the gradient, we can control the phase angle by varying the amplitude (A-D) and polarity of the gradient (+A, -A).
Frequency and phase encoding are very closely related.
The main difference between the two methods is that the phase encoding is completed before the start of the measurement of the signal, whereas frequency encoding is applied during the measurement process.
In frequency encoding, we can use the evolution of signal with time to give us the desired number of points; in the phase-encoding direction, we do not have this option and hence have to repeat the experiment.